Insert Audio (Sound) in PowerPoint 2003 and 2002 for Windows

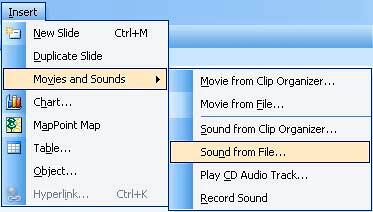
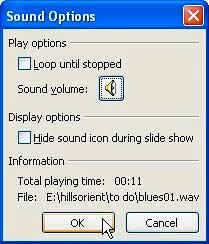
There are many ways to bring in sounds in PowerPoint. You can insert event sounds, transition sounds, or as we are going to show you now: inserted sounds.

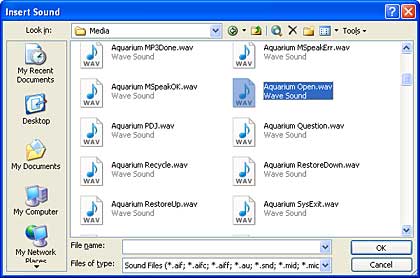
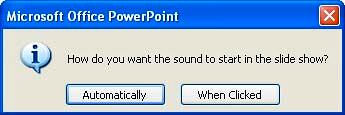
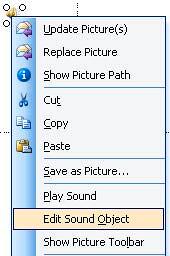
Follow these steps to insert sound in PowerPoint 2003 or 2002 (XP) for Windows:

1. In PowerPoint, navigate to the slide where you want the sound to be inserted.
2. Choose the Insert | Movies and Sounds| Sound from File menu option, as shown in Figure 1, below.
3. 
   Figure 1: Choose a sound to insert
3. Doing so will summon the Insert Sound dialog box that you can see in Figure 2, below. Navigate to the folder where your sound clips are saved, and choose the sound file you want to insert, and then click the OK button.
4. 
   Figure 2: Insert Sound

Compatible Audio File Formats

Remember that PowerPoint only allows you to insert a limited range of sound file types such as WAV, MP3, WMA, MIDI, AIFF, etc. If you need to insert a sound in another format, you'll have to convert it to a format that PowerPoint accepts. Also, look at our PowerPoint Friendly Audio Formats page to understand which common and exotic audio file types you can insert in your PowerPoint slides.
4. This action will get you back to your slide. PowerPoint prompts you with a dialog box, as shown in Figure 3, below, asking whether the sound to play Automatically or When Clicked in the slide show.
5. 
   Figure 3: Placed sound on a slide
6. If you choose Automatically, PowerPoint will play the sound the instant that the slide containing the sound is shown in slide show view.
7. If you choose When Clicked, the presenter will have to click on the audio icon that PowerPoint places on the slide to play the sound.
5. Whichever option you choose, PowerPoint will place an audio icon on the center of the slide. You can right-click this audio icon, which displays the menu, as shown in Figure 4, below. To look at more advanced options, choose the Edit Sound Object option, as shown in Figure 4.
6. 
   Figure 4: Edit Sound Object
6. Doing so opens the Sound Options dialog box, as shown in Figure 5, below. Options in this dialog box allow you to change the sound volume, make the sound loop, hide the sound icon during slide show, etc. You'll also be able to find out how long the sound plays, and the path to the the sound file.
7. 
   Figure 5: Sound Options
7. After making changes, click the OK button to apply the changes. Play your presentation to test the sound.