Animation Painter in PowerPoint 2010 for Windows

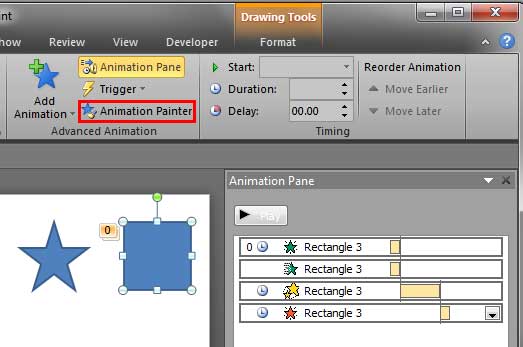
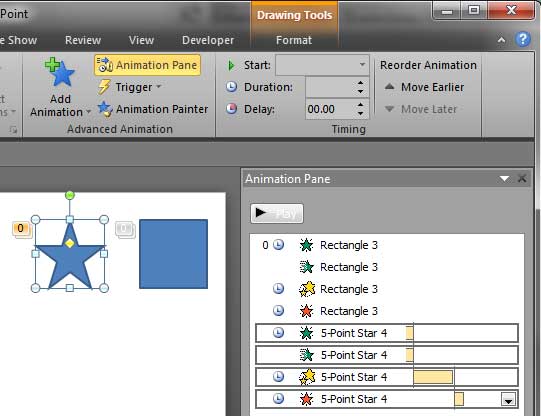
Let's imagine you got your animation just right. You tweaked the speed, set the animation events, etc. You also added a series of simultaneous and sequential animations to the same slide object. So, that it fades and wipes at the same time. Then it grows in size, stays on screen without animation for a requisite amount of time (delay) and finally the object exits using a simple fade animation. Now, you need to apply the same animation to 50 other slide objects within the presentation! Typically, you may have to spend an enormous amount of time for such a repetitive task, manually applying the animations so many times! That was before the introduction of the new Animation Painter feature, introduced in PowerPoint 2010, which works with animations exactly in the same way as Format Painter option works with slide objects. So what does the Animation Painter command do? Here are some answers:

• Animation Painter copies animation attributes from one slide object.
• You can then apply the same animation attributes to another slide object on the same slide, the same presentation, or across presentations.
• You can also copy the animation attributes to multiple slide objects similarly.

Follow these steps to explore how you can use the Animation Painter in PowerPoint 2010 for Windows:

1. Select the slide object whose animation attributes you want to copy, as shown in Figure 1, below. Note that we selected the Rectangle shape, and you can see that several animations have been applied to this shape, as shown in the Animation Pane in Figure 1. Also note that the Star shape has no animation applied to it.
2. 
   Figure 1: Shape applied with multiple animations selected
2. Now, access the Animations tab of the Ribbon. Click the Animation Painter button, as shown highlighted in red within Figure 1, above.
3. This will change the cursor to a Paintbrush icon, as shown highlighted in red within Figure 2, below.
4. 
   Figure 2: Cursor changed to a Paintbrush icon
4. Now, just click on the other shape to which you want all animation attributes of the original slide object to be copied. We clicked the Star shape, as shown in Figure 3, below.
5. 
   Figure 3: Animation attributes copied and applied to the other shape
5. If you want to copy and apply animation attributes to more than one slide object, first double-click the Animation Painter button (rather than a single-click) so it remains selected. Thereafter, you can click on any number of slide objects you want. When you are done with copying and applying animations, click the Animation Painter button again, or just press the Esc key to restore your cursor to the normal editing mode.
Tip:
You do not have to click with the Animation Painter's Paintbrush icon only on the slide objects within the same slide. You can click on any slide object, on any slide, and within any presentation as long as the presentations containing the source object and destination object are open at the same time.
6. Save your presentation often.